1. 서론
태풍은 산사태, 호우 그리고 폭풍해일과 같은 현상을 동반하며 막대한 사회경제적인 피해를 일으키는 재해요소로서 고도화된 사회에서도 그 영향을 피할 수 없는 국가적인 재해요소이다(Needham et al., 2015; Nolasco-Javier and Kumar, 2018; Rappaport, 2014; Syvitski et al., 2014). 재해를 줄이기 위해 세계 각국은 태풍에 대한 감시와 예측에 대한 노력을 지속적으로 기울이고 있다. 기존 연구에 따르면 태풍은 엘니뇨 환경에서 증가하며(Kang et al., 2019; Wang and Chan, 2002), 온난한 환경에서 감소하는 경향을 보이는 것으로 나타난다(Chou et al., 2013; Kang and Elsner, 2016; Sugi and Yoshimura, 2012). 한편, 아직 북서태평양 태풍에 대한 연구는 북반구 태풍의 활동이 활발한 대략 6개월 기간(6~11월)에 대해 집중해 있어 계절간 특성에 대한 이해가 부족한 상황이다. 본 연구는 계절 단위의 태풍의 수가 기후환경에 어떻게 반응하는지를 분석함으로써 계절 특성을 보다 깊이 이해하고자 하였다.
우선, 전지구 해역마다 태풍에 대한 명칭이 다양하여 논문과 보고서 등에서 다룰 때 그 정의를 분명히 할 필요가 있다. 서술에 앞서, 본 논문에서는 중심최대지속풍속이 17 ms-1으로 기록된 열대저기압을 “태풍”으로 표현함을 밝힌다. 이는 World Meteorological Organization(2022) 기준으로 열대폭풍(Tropical Storm) 이상의 강도를 갖는 열대저기압을 우리나라, 일본, 대만 등에서 관례적으로 “태풍”이라 통칭해 옴에 따라 용어에 대한 국내독자의 이해를 돕기 위한 것이다(강남영, 2023).
태풍은 다양한 시간규모에 대한 분석이 가능하다. World Meteorological Organization(2021)는 단기, 중기 그리고 장기로 시간규모를 구분하고 있으며 대부분의 기상 및 기후정보도 이러한 규모들로 분류되어 다루어진다. 단기는 하루에서 이틀 사이, 중기는 사흘에서 열흘 사이, 그리고 장기는 주로 한달 이상의 기간을 표현하고 있다. 장기의 기간 중에서도 태양의 천문학적인 활동으로 인해 발생하는 주기적인 계절의 진동을 3개월 단위로 다루고 있다. 한편, 중기와 계절의 사이의 시간 규모를 “계절안(sub-seasonal)”으로 표현하는데 이는 수치역학모델의 예측성능이 충분히 미치지 못하는 구간으로서 많은 연구자들의 도전 대상이다(Chen and Alpert, 1990; Slingo et al., 1996). 이는 대기와 해양의 기후환경의 조건들이 각기 다른 관성을 가지고 있고 이를 구현하는데 있어서 어려움을 겪고 있기 때문이다(Robertson et al., 2020; Vitart and Robertson, 2018). 계절안 규모에서 태풍 발생수의 기후 반응을 보다 깊이 이해할 수 있다면 역학모델 등 다양한 도구들의 예측성능 개선 노력에 도움을 줄 수 있을 것이다.
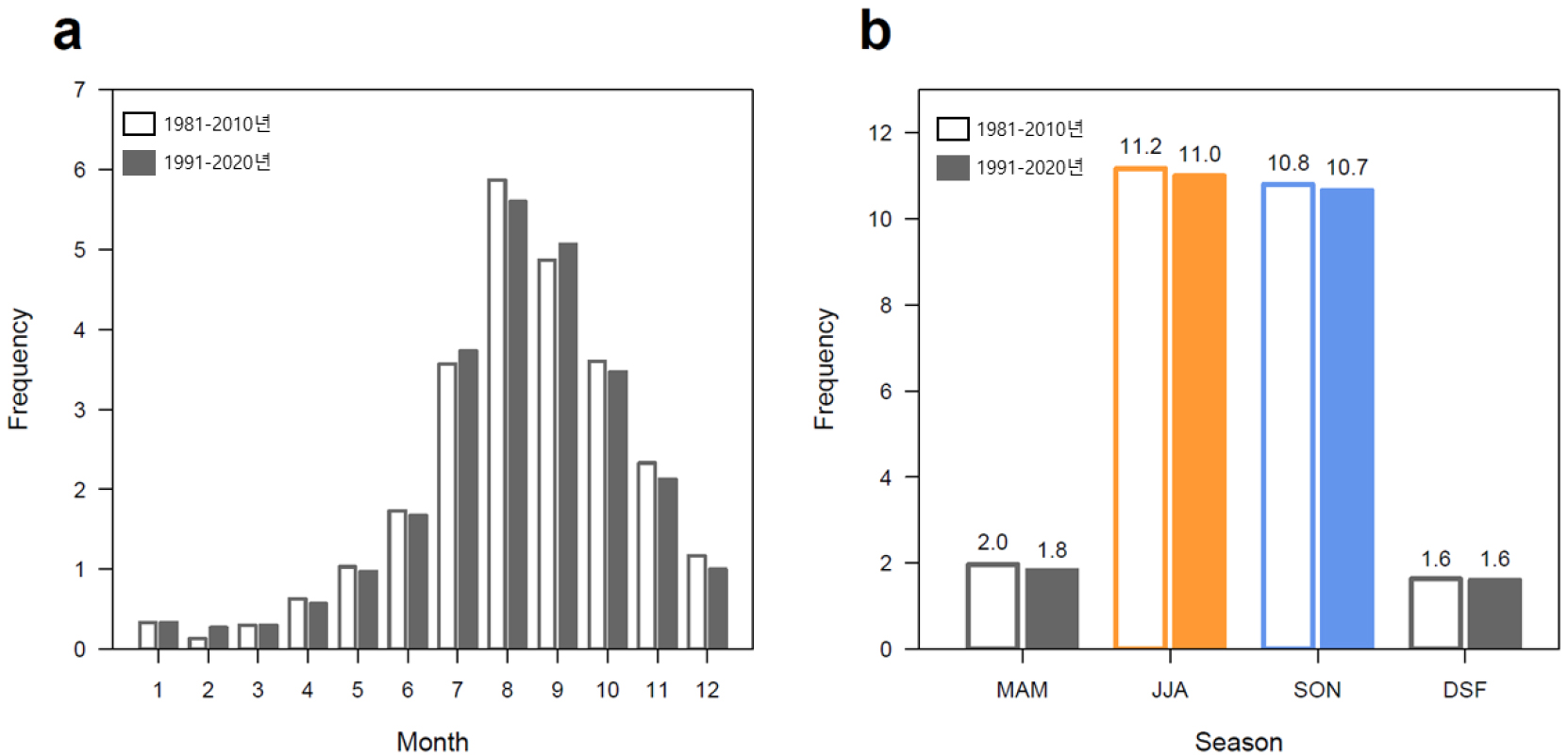
그림 1은 북서태평양의 월별 태풍 발생수를 보여준다. 이는 30년 평년기간의 기상청 관측 값을 사용한 것이다. 일반적인 경향을 파악하기 위해 이전 평년기간(1981~2010년)과 현재 평년기간(1991~2020년)의 값들을 함께 표출하였다. 태풍 발생수의 최대치는 8월에 나타나지만 9월의 발생수도 8월과 큰 차이를 보이지 않을 만큼 높은 수준이다. 북반구 태풍 활동이 활발한 6~11월 태풍 발생수가 22.0개(1981~2010년)와 21.7개(1991~2020년)로서 여름철과 가을철은 태풍 활동의 성수기라고 할 수 있다. 두 계절의 태풍이 전체의 85.9%(1981~2010년)와 86.3%(1991~2020년)를 차지할 정도로 여름철과 가을철은 한 해 태풍의 활동을 대표한다고 볼 수 있다. Kang and Elsner(2016)는 성수기 태풍의 발생수의 경년 변동이 엘니뇨-남방진동과 지구온난정도에 크게 영향을 받고 있음을 보였다. 태풍의 발생은 따뜻한 해의 라니냐 환경에서 감소하며, 반대의 환경에서는 증가하는 경향을 드러내는 것이다. 한편, 이는 한해 대표적인 두 계절 기간 동안의 활동도를 분석한 것으로서, 아직 두 계절 간의 차이를 살펴본 연구는 찾아보기 어렵다. 두 계절의 태풍 발생수를 비교해 보면 여름철과 가을철의 수가 거의 비슷한 수준으로 나타나고 있어, 어느 해 두 계절 태풍 발생수 간의 차이가 발생한다면 이는 선형적인 관점에서 각 계절내에서의 증가 또는 감소에 따른 것으로 해석할 수 있다. 본 논문은 태풍 발생수에 관여하는 이러한 계절안 규모의 변화 특성을 “계절안 변동성(sub-seasonal variability)”이라 정의하고 이러한 계절안 변동성이 계절별 태풍 발생수의 경년 변동에 어떻게 관여하고 있는지를 통계적으로 분석하고자 하였다. 이를 위해. 엘니뇨-남방진동과 지구온난정도를 활용하여 복합적인 기후환경을 지표화하고, 태풍 발생수의 계절 편차가 이에 어떻게 반응하는지를 살펴봄으로써 궁극적으로 계절안 변동성이 계절별 태풍수 결정에 영향을 미치는 구조를 파악하였다. 이는 사실상 연간 태풍 발생수의 경년 변동과 계절규모의 경년 변동을 구분하는 진단적 기술로서, 태풍 발생수에 대한 계절예측 모델링을 개선하기 위한 기반을 마련한다는 점에서 의미를 갖는다.
본문의 구성은 다음과 같다. 2장은 분석에 사용된 관측자료를 소개하였다. 3장에서는 태풍 발생수의 계절 편차와 계절안 변동성의 개념을 정의하고 이들의 반응을 분석하기 위한 기후환경에 대해 설명하였다. 이어서, 4장은 분석 결과를 소개하며, 5장에서 논문의 내용을 요약하고 의미를 기술하였다.
2. 자료
본 연구의 분석대상은 북서태평양의 태풍 발생수이다. 이는 기상청 국가태풍센터의 관측값을 사용하였다. 기후환경 조건에 따른 태풍 발생수 반응 분석은 여름철(6~8월, JJA), 가을철(9~11월, SON), 성수기(6~11월, JJASON)를 대상으로 하였다. 여기서 ‘기후환경’은 태풍의 기후적 특성의 배경이 되는 주변 조건을 의미한다. 기후환경을 지표화하기 위해 사용되는 엘니뇨-남방진동(El Nino-Southern Oscillation, ENSO)과 전지구 온난정도는 각각 남방진동지수(Southern Oscillation index, SOI)와 전지구 평균 해수면온도(Global mean sea-surface temperature, GMSST)를 활용하였다. SOI는 미 해양대기청 기후예측센터의 자료(CPC; www.cpc.ncep.noaa.gov/data/indices/soi)를 바로 이용하며, GMSST는 미 해양대기청 환경예측센터로부터 얻은 해수면온도확장판(ERSST v5) 자료로부터 위도별 면적을 가중하여 산출하였다. SOI의 양의 값은 라니냐 경향을 의미하는데, 본 논문은 엘니뇨를 양의 값으로 다루기 위해 음의 SOI를 의미하는 NSOI(negative SOI)를 지표로 다루었다. 전 지구 평균 해수면온도는 해양의 직접 물리변수임과 동시에 전 지구 온난정도를 가리키는 지표로서 사용된 것이다(Kang and Elsner, 2015).
본격적인 분석에 앞서 분석의 기간을 정해야 한다. 결과를 일반화하기 위하여 가능한 긴 기간에 대해 분석을 수행하기 마련이지만, 이는 기후환경과 태풍의 관계가 안정되어 있다는 가정에 따른 것으로서 많은 표본을 통해 보다 확실한 관계를 추정하기 위한 방법이다. 한편, 최근 연구에 따르면 기후환경과 태풍의 관계가 이전과 차이를 보이는 것으로 나타났다. Kang et al.(2023)은 대략 2013년 이후 기간에서 환경조건에 따른 태풍의 반응이 이전과 다르게 관측되고 있다고 밝히고 있다. 환경-태풍 간의 물리적 구조가 바뀌지 않았다고 가정할 때 이는 외부 간섭에 따른 왜곡이 일정기간 나타나고 있는 것으로 이해할 수 있으며, 따라서 상대적으로 간섭이 적었던 기간의 표본을 통해 이전의 기후관계를 확인하는 것을 최선으로 생각할 수 있다. 이러한 부분을 고려하여 본 연구는 우선 환경-태풍간의 안정된 기후관계가 확인된 28년(1985~2012년)의 기간을 대상으로 분석을 수행하였다.
3. 방법
1) 태풍 발생수의 계절 편차
연간 태풍 발생수를 FRQ(Frequency)로 나타냈다. 여름철(6~8월), 가을철(9~11월), 성수기(6~11월)의 태풍 발생수를 FRQJJA, FRQSON과 FRQJJASON로 표시한다면 다음과 같은 기본적인 수식으로 서로의 관계를 표현할 수 있다.
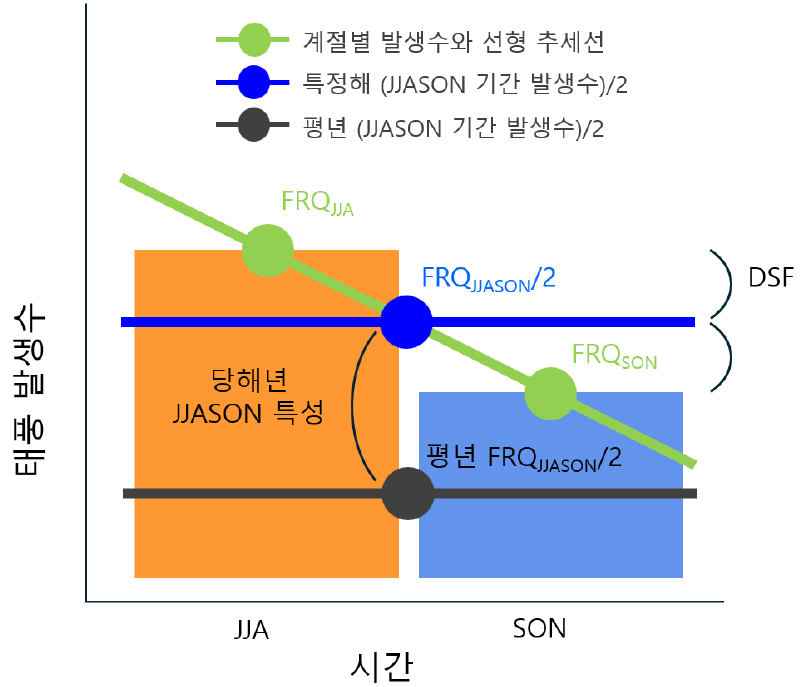
성수기 태풍 발생수인 FRQJJASON는 두 계절의 발생수를 더한 것으로 간단히 이해된다. 그림 2는 태풍 발생수의 계절 분포와 값들 사이의 관계를 보여주는 모식도이다. 어느 해 태풍의 수가 많거나 적은 것은 대부분 성수기의 발생수인 FRQJJASON의 경향을 따른다고 볼 수 있다. 두 계절의 평균인 FRQJJASON/2가 평년 수준과 비교하면 어느 정도인지를 통해 성수기 태풍의 특성을 파악할 수 있다. 한편, FRQJJA와 FRQSON는 그 해 성수기 태풍의 특성에 그 해의 계절적 특성이 더해진 결과로 이해된다. 즉, 그 해 JJA의 특성은 계절 편차(deviation of seasonal frequency, DSF)의 크기로 이해할 수 있다. 이에 따라, 본 연구는 태풍 발생수의 계절 편차(DSF)를 다음과 같은 수식으로 정의하고자 한다.
편의상 JJA의 계절 편차를 DSF로 정의하지만, 사실상 SON의 계절 편차도 DSF와 부호만 다를 뿐 같은 크기를 갖는 값이다. 구조상 DSF의 절대 값이 크게 나타날수록 두 계절 간 값의 차이가 커지며, 이는 선형적으로 볼 때 JJA와 SON 각각의 내부 기울기를 동반하게 된다. 여기서 ‘내부 기울기’란 JJA 및 SON 시간 규모안에서의 증가 또는 감소 추세를 의미한다. 다시 말해, 계절 편차는 계절안 규모의 변화가 있기에 나타나게 된다. 본 연구는 태풍 발생수에 관여하는 이러한 계절안 규모의 변화 특성을 “계절안 변동성(sub-seasonal variability)”이라 정의하고, DSF를 분석함으로써 이러한 계절안 변동성이 JJA와 SON의 태풍 발생수에 어떻게 영향을 미치는 지를 살펴보고자 한다.
그림 3a는 본 연구의 분석 대상인 1985~2012년 기간 동안 JJA, SON, JJASON의 태풍 발생수를 시계열로 나타낸 것이다. FRQJJA와 FRQSON이 서로 교차하며 변동하고 있으며, 변동의 폭이 커서 계절 태풍 발생수의 크기가 어느 수준인지 특정짓기 어렵다. 앞서 설명한 대로, FRQJJASON은 성수기의 태풍 발생수로서 FRQJJASON/2는 계절 규모의 변동을 보여주는 시계열이다. 여기서 FRQJJA와 FRQJJASON/2의 차이는 FRQSON과 FRQJJASON/2의 차이와 부호만 다를 뿐 구조적으로 같은 절대 값의 크기를 갖는다. 그림 3b는 FRQJJA와 FRQSON으로부터 성수기 태풍 발생수의 변동을 제거한 결과를 보여준다. 이는 계절 편차만을 시계열로 표출한 것으로서, JJA의 계절 편차로 정의된 DSF가 음영으로 처리되어 있다. 평년 기후 값에서 보았듯이(그림 1b), JJA와 SON의 태풍 발생수가 비슷한 수준임에 따라 DSF의 수치가 음과 양의 부호를 오르내리며 변동하는 이유를 알 수 있다. 결과적으로 DSF가 음의 값으로 나타난 해는 계절안 변동성의 영향으로 가을철의 태풍 발생 수가 여름철 보다 증가한 경우이며, 반대로 양의 DSF가 나타난 해는 여름철을 지나 가을철에 태풍의 발생 수가 줄어든 경우를 의미한다. DSF의 크기는 계절 간 변화의 폭이 얼만큼 큰지를 보여준다.
태풍 발생수의 계절 분포를 입체적으로 이해하기 위해 본 연구는 Kang and Elsner(2016)의 연속변동공간의 개념을 활용하였다. 연속변동공간은 두개의 기본변수들과 그에 따른 두개의 주성분들로 연결된 변동공간으로서, 본 분석에는 가로 축과 세로 축에 각각 DSF와 FRQJJASON를 적용한다. 두개의 두 주성분들은 아래 수식과 같이 계산할 수 있다.
여기서 ‘s( )’는 표준화 연산자를 표시한 것이다. PC1은 DSF와 FRQJJASON의 동위상 변동성에 대한 수식이며 DSF와 FRQJJASON가 동시에 높은 수준일 때 높은 값을 나타낸다. 한편, PC2는 DSF와 FRQJJASON의 역위상 변동성을 표현한 수식으로서 DSF는 높으면서도 동시에 FRQJJASON가 낮은 수준인 경우를 가리킨다. 표준화 연산의 특성상 s(FRQJJASON)은 s(FRQJJASON/2)와 같은 것으로서 앞서 계절 편차를 계산하기 위해 다루어진 성수기 태풍 발생수의 변동을 그대로 의미한다.
2) 기후환경 조건 정의
본 연구는 DSF의 경년 변동이 기후환경에 어떻게 반응하는지를 분석하고자 한다. DSF를 설명하기 위한 환경조건을 크게 내부진동과 외부강제력으로 구분할 수 있다. 정의상 내부진동은 태풍을 발생시키는 환경에 새로운 힘이 가해지지 않고서도 현상이 자연스럽게 진동하는 것이며, 외부강제력은 환경안으로 유입되어 현상 자체를 변화시키는 새로운 힘을 의미한다(Kang and Elsner, 2015). 여러 내부진동들 중에서도 ENSO는 전지구 해양과 대기가 연동되어 기후환경의 상당부분을 설명하는 기후환경이다(Ashok et al., 2007). 또한, 지구온난화는 여러 외부강제력 중에서도 최근 환경의 변화를 설명하는 대표적인 기후현상이다. 태풍 발생 성수기의 기후 환경에 대한 연구는 많이 이루어져 있다. 엘니뇨 환경에서 무역풍의 약화로 해수의 고온 편차역이 동쪽으로 이동하고(Bjerknes, 1966), 이로써 주요 태풍 발생지역은 북서태평양의 남동부 해역에 나타난다(An, 2018; Wang and Chan, 2002). 이는 사실, 태풍 발생지역이 옮겨간 것 보다는 해당 지역의 태풍이 더 많이 발생한 데 따른 것으로서 결과적으로 전체 태풍 발생수를 증가시키는데 기여한다(Kang et al., 2019). 온난한 시기에는 가열된 해수면에 보다 많은 수증기가 증발하여 높은 습윤정지에너지를 보임에도 불구하고, 중・상층 대류권이 고온 건조해짐으로써 상향 질량속의 감소, 즉 태풍 발생 억제 효과를 가져오게 된다(Chou et al., 2013; Kang and Elsner, 2016; Sugi and Yoshimura, 2012). 한편, 이러한 물리적인 이해는 연간 또는 6개월 기간 정도의 시간규모에 대한 것이어서 계절 간의 차이를 구분하여 설명하지는 못한다. 본 연구의 결과는, 이러한 ENSO의 영향이 여름철에 더 크게 영향을 미치며, 온난화의 영향은 가을철에 더 잘 드러난다는 것을 의미하는 것으로서, 향후 계절안 규모를 포함한 작은 시간 규모에서의 반응을 세분화하여 파악할 필요가 있음을 시사한다. 본 연구는 ENSO와 지구온난화를 대표적인 두 기후환경으로 선정하고 이들이 조합된 기후환경 조건이 DSF에 어떻게 영향을 미치는지를 분석하였다. ENSO의 지표로는 NSOI를 사용하고자 한다. NSOI는 SOI의 부호를 반대로 함으로써 엘니뇨 경향이 양의 값으로 표현되도록 한 것이다. 지구온난화의 지표로는 전지구 해양의 온난정도를 나타내는 GMSST를 사용한다. GMSST는 전지구 기온과 매우 비슷한 경향을 보이면서도 태풍 발생에 보다 직접적으로 관련된 물리적 변수라는 점에서 유용한 지표이다(Kang and Elsner, 2015; 2016).
4. 결과 및 해석
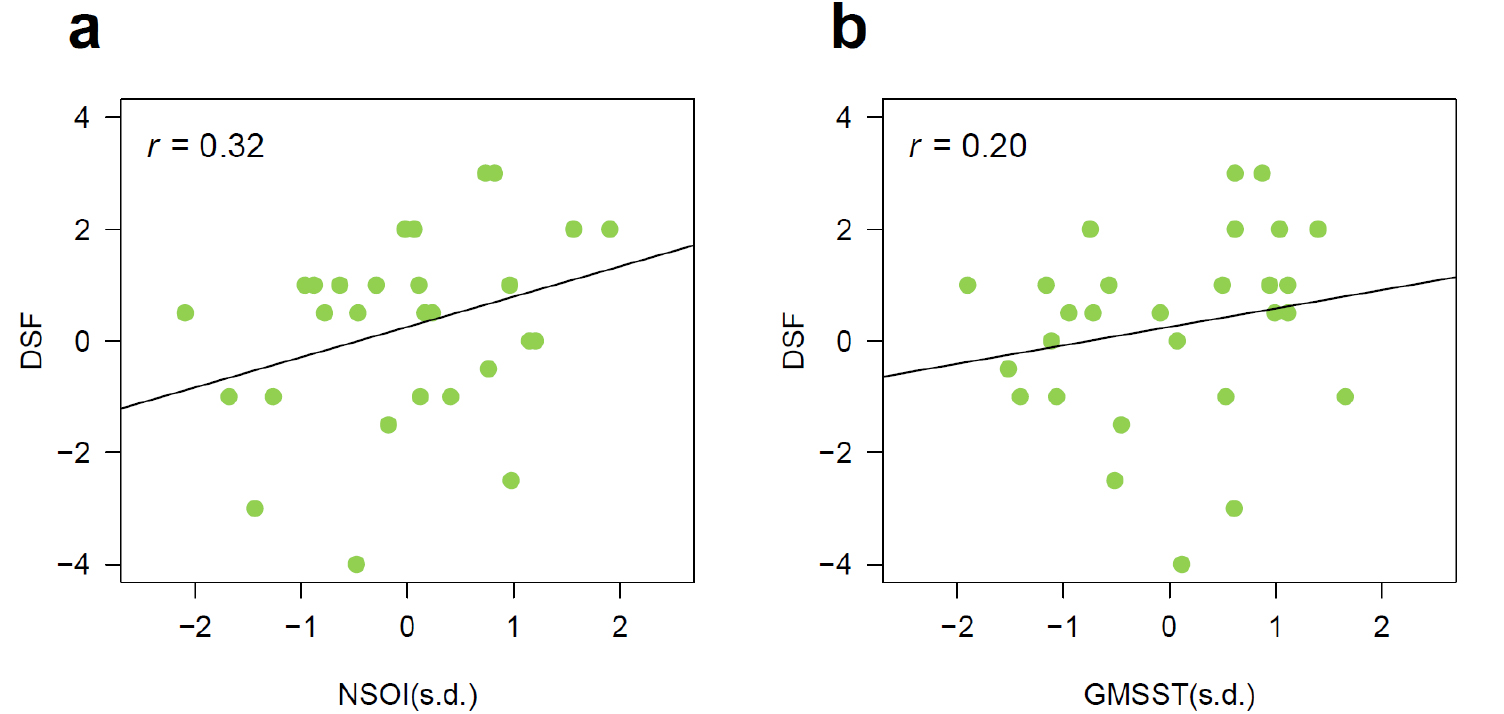
NSOI와 GMSST 지표들을 사용하여 기후변동과 기후변화에 따른 DSF의 반응을 분석하였다. 그림 4은 연간 DSF와 NSOI의 관계 및 GMSST의 관계를 보여준다. DSF는 NSOI와 양의 상관을 보이는 것으로 나타났다. 95% 신뢰수준에는 미치지 못하지만, 90% 신뢰수준으로 유의한 상관을 갖는다(r = +0.32; [0.00, 0.58], 90% 신뢰구간). 다시 말해, 어느 해 JJASON 기간 기후환경이 엘니뇨 경향을 보일 때 여름철 태풍 발생수의 계절 편차가 크게 나타날 가능성이 있다는 것이다. 이는 SON의 태풍 발생수가 JJA 기간을 지나 감소할 가능성이 있다는 의미이다. 한편, DSF와 GMSST는 유의한 상관을 보이지 않았다(r = +0.20; [-0.13, 0.48], 90% 신뢰구간. 태풍 발생수의 계절 편차가 지구온난화에 양의 반응을 보이긴 하지만 그 정도가 95%이나 90% 신뢰수준에서 모두 유의하게 나타나지는 않는 것이다.
한편, 이는 DSF의 관점을 고정한 결과를 본 것일 뿐 태풍 발생수의 반응 전체를 이해한 것은 아니다. 그림 5a는 360°전 방향으로 표현된 연속 변동공간에서 NSOI가 각 변동 방향과 어느 정도의 상관도를 갖는지 계산 결과를 보여준다. 안쪽 원과 바깥 원은 각각 상관도 0.5와 1.0을, 원의 중심은 0.0을 가리킨다. 유의성 분석을 통해 90% 신뢰수준으로 유의한 상관도를 보이는 구간을 붉은 색 두꺼운 실선으로 표현하였다. 엘니뇨 경향에 따른 최대 반응은 PC1에 가까운 것으로 나타난다(r = +0.55; [0.17, 0.68], 90% 신뢰구간). 동위상 관계가 설명하듯 이는 엘니뇨 경향의 해에 두 계절 태풍 발생수의 격차(FRQJJA-FRQSON) 규모가 커짐과 동시에 FRQJJASON 전체가 함께 커지는 경향이 DSF나 FRQJJASON의 개별 반응보다 더욱 뚜렷하게 나타난다는 것을 의미하는 것이다. 이는 구조적으로 FRQJJA의 증가가 엘니뇨에 가장 유의하게 반응한다는 것을 암시한다. 종합적으로 보면, 엘니뇨 경향의 기후환경 조건은 여름철 태풍 발생수의 수준이 높아 가을철 태풍 발생수와의 격차가 큼에도 불구하고 성수기 전체 태풍 발생수를 높은 수준으로 유지시킨다고 해석할 수 있다. 앞선 그림 4a의 결과는 그림 5의 관점에서 볼 때 사실상 유의 구간의 가장자리에서 가까스로 세로 축에 걸친 단편적인 값이었음을 이해할 수 있다. 같은 결과를 라니냐의 경향으로 해석해본다면 거울처럼 뒤집어진 -PC1 부근의 방향에서 반응이 최대로 나타나는 것을 볼 수 있다. 이는 라니냐 경향의 기후환경 조건이 가을철 태풍 발생수와 여름철 태풍 발생수의 격차(FRQSON-FRQJJA)를 키움과 동시에 전반적인 FRQJJASON 감소를 야기하는 것을 의미한다. 이는 구조적으로 FRQJJA의 감소가 라니냐에 가장 유의하게 관련되어 있다는 것을 암시한다. 이로써, 라니냐의 환경은 여름철 태풍 발생수를 줄임으로 인해 가을철 태풍 발생수가 증가하는 것처럼 여겨지게 하지만 전체적으로는 성수기 태풍 발생수의 감소를 야기하고 있다. 이처럼, ENSO는 여름철 태풍 발생수에 깊이 관여함으로써 성수기 태풍 발생수의 증감에 영향을 미침과 동시에 계절안 규모의 변화를 통해 계절 태풍 발생수의 차이를 만들어내고 있는 것이다.
그림 5b는 동일한 분석틀을 GMSST에 적용한 결과이다. 지구가 온난한 해일 수록 가장 큰 반응을 보이는 방향이 PC2에 가깝다는 것을 보여준다(r = +0.58; [0.26, 0.73], 90% 신뢰구간). PC2가 역위상 관계를 의미하듯이 이는 온난할수록 DSF의 증가와 FRQJJASON의 감소가 동시에 나타나는 변동성이 가장 뚜렷한 반응을 보인다는 것을 말한다. 이는 구조적으로 FRQSON의 반응을 의미한다. 온난한 기후환경 조건이 FRQSON의 크기를 줄임으로써 성수기 태풍 발생수 전체의 수준을 낮추고 계절 간 격차도 키우게 되는 것이다. 즉, 지구온난화에 따른 연간 태풍 발생수의 감소(Kang and Elsner, 2016)와 계절 분포가 가을철 태풍의 수의 감소 때문이었음을 통계적으로 보여주는 결과이다. 근원적으로 전지구 온난정도와 ENSO는 각각 외부강제력과 내부진동으로서 긴 시간에 걸쳐 서로 무관한 변동성을 갖는다. 내부진동은 외부로부터의 힘이 가해지지 않았기 때문에 결국 제 자리로 돌아오지만, 외부강제력은 새로운 힘으로 이전의 상태를 바꾸는 것이어서 둘의 시간변화는 서로 상관이 없게 되는 것이다. 이는 실제 기후환경 조건을 지구 온난정도와 ENSO의 선형적인 조합으로 이해할 수 있도록 한다(Yun et al., 2023). 따뜻한 해의 엘니뇨 환경, 따뜻한 해의 라니냐 환경, 차가운 해의 엘니뇨 환경, 차가운 해의 라니냐 환경 등 다양한 실제 기후환경 조건을 구성한다면 연간 태풍 발생수의 특성을 보다 실질적으로 이해할 수 있을 것이다. 선형적인 관점에서 ENSO와 지구온난정도를 각각 내부진동과 외부강제력의 지표로 두고 그 결과를 해석한다면, 특히 더욱 따뜻한 미래 환경에서 라니냐 해에 가을철 태풍수의 큰 감소에 따른 전체 태풍수의 감소를 경험하게 될 가능성이 높아진다고 볼 수 있다. 본 연구는 간단한 구성을 통해 계절안 규모의 변동성, 계절 편차, 계절 간의 격차, 성수기 전체 태풍 발생수가 기후환경 조건에 어떻게 반응하는지를 입체적으로 이해하고자 하였다. 이는 향후 보다 실제적으로 조합된 기후환경에 따른 태풍 발생수의 반응을 효과적으로 이해하는 바탕이 되어줄 것이다.

그림 5.
계절 태풍 발생수 관련 변수들의 기후환경 조건에 대한 반응. (a) SOI 와 (b) GMSST의 상관도 분포. 연속 변동공간은 DSF와 FRQJJASON를 각각 가로 축과 세로 축의 변수로 두고 동위상 변동성을 나타내는 주성분인 PC1과 역위상 변동성을 나타내는 주성분인 PC2를 연결한 것이다. 각 방향은 변수들이 서로 다르게 가중된 영향을 미치는 변동성을 가리킨다. 연속 변동공간의 개념과 형식은 Kang and Elsner(2016)을 따랐으며, 분석은 28년(1985~2012년) 기간의 자료를 대상으로 하였다.
5. 요약 및 토의
태풍은 자연재해 중에서도 가장 큰 피해규모를 갖는 현상으로서 북서태평양에서는 주로 여름철과 가을철에 많은 발생수를 기록한다. 기후 평년기간의 통계에 나타나는 북서태평양 여름철과 가을철의 연평균 태풍 발생수는 비슷한 수준인 것으로 나타나지만 해마다 그 수는 경년 변동을 보이며 오르내리기를 반복한다. 일반적으로 어느 해 태풍의 활동이 활발했는지를 파악하는데 있어 이 두 계절의 태풍 발생수가 전체적으로 어떠했는지를 비중있게 다루지만, 두 계절 간의 차이를 깊이 살펴본 연구는 쉽게 찾아보기 어렵다. 본 연구는 평균적으로 비슷한 수준인 두 계절의 빈도 사이에 연간 차이가 발생하는 것은 구조적으로 계절안 규모의 변동에 따른 것이라고 가정하였다. 이어, 각 계절의 태풍 발생수가 두 계절의 평균과 갖는 차이를 계절 편차로 정의하고, 연간 성수기 태풍 발생수와 계절 편차를 기본 변수로하는 연속 변동공간을 구성하였다. 여기서 계절 편차는 계절안 변동성이 계절 간의 격차를 만드는 과정을 의미하는 것으로서 변동공간을 입체적으로 구성하기 위해 사용된 것이다. Kang and Elsner(2015)의 분석틀을 계절 태풍 발생수에 적용한 이 연속 변동공간은 여름철과 가을철의 태풍 발생수, 두 계절이 종합된 성수기 태풍 발생수, 그리고 계절안 변동성의 영향에 따른 두 계절 간의 차이를 한 번에 파악하기 위한 도구로 활용되었다. 연속 변동공간의 반응을 살피기 위한 기후환경 조건을 내부진동과 외부강제력으로 나누고 ENSO와 전지구 온난정도를 각각의 설명변수로 삼았다. 논문에서는 여름철 태풍 발생수가 가을철 태풍 발생수보다 큰 경우를 양의 계절 격차 부호로 설정하였다. 우선, 엘니뇨의 경향이 커질수록 성수기 태풍 발생수와 두 계절 간 격차가 동시에 커지는 경향이 뚜렷하게 드러남을 확인하였다. 라니냐의 경향은 반대 방향의 변동성을 따름으로써 성수기 태풍 발생수를 줄임과 동시에 두 계절 간의 격차를 키우는 경향이 뚜렷하였다. 다시 말해, 엘니뇨와 라니냐 경향은 각각 여름철 태풍 발생수의 증가와 감소에 보다 깊이 관여함으로써 연간 태풍 발생수 특성에 전반적인 영향을 미치고 있다는 것을 파악하였다. 한편, 전지구 온난정도가 커질 수록 성수기 태풍 발생수의 감소와 계절 편차의 커짐이 함께 나타나는 특성이 뚜렷하게 나타났다. 이는 지구온난화가 가을철 태풍 발생수의 감소에 보다 깊이 관여함으로써 계절 격차는 물론 성수기 태풍 발생수를 감소시키고 있다는 점을 보여주는 결과로 해석된다. 한편, 태풍의 지역 영향은 전체 태풍의 발생수 뿐 아니라 진로 특성에 크게 영향을 받고 있어(Park et al., 2006), 향후 한반도 영향에 대한 연구는 발생수와 진로를 함께 고려할 필요가 있다.
본 연구는 내부진동과 외부강제력에 따른 연간 태풍 발생수의 변동을 분석하였으며, 태풍 발생수에 관여하는 값들을 연속 변동공간에 표현함으로써 결과를 입체적으로 이해할 수 있었다. 사실상 기후환경 조건은 내부진동과 외부강제력의 다양한 조합으로 나타난다(Yun et al., 2023). 본 논문의 결과와 해석 방법은 엘니뇨와 라니냐의 규모와 주기성, 수온 상승의 폭과 변동성 등을 정량적으로 표현함으로써 향후 실제 기후환경을 활용한 태풍 발생수 계절예측모델을 구축하거나 개선하는데 도움을 줄 수 있을 것으로 기대된다. 또한, 연구의 결과는 미래기후를 예측하는 역학모델의 태풍 기후를 해석하는데 유용하게 사용될 수 있을 것으로 사료된다.