1. 서론

지리학을 “공간적 상호작용의 과학”이라고 정의한 에드워드 울만(Edward L. Ullman)의 생각을 온전히 받아들이지는 않는다 하더라도(Ullman, 1980, 30), 지리학이 공간적 상호작용 연구에서 길고도 깊은 전통을 가지고 있다는 사실을 부인하는 지리학자는 별로 없을 것이다. 공간적 상호작용을 “공간상의 지점들 간의 모든 종류의 흐름”이라고 단순하게 규정할 수 있다고 했을 때(이상일, 2012), 여기에 포함되는 현상에는 인구이동, 통근, 물류와 같은 다소 전통적인 의미의 것들뿐만 아니라, 소셜미디어(social media)를 통한 개인간 소통 양상, COVID-19의 사례가 보여주는 글로벌 차원의 병원균 전파와 같은 새로운 것들도 포함된다. 위치부착 정보(geotagged information), 혹은 다양한 종류의 자발적 지리정보(volunteered geographic information, VGI)(Sui et al., 2012)가 넘쳐나고 있는 현 상황을 고려할 때, 공간적 상호작용 연구는 새로운 도약의 계기를 맞고 있다고 볼 수 있다. 이러한 측면에서 공간적 상호작용과 관련된 다양한 방법론적 과제들을 면밀히 검토해야 할 필요성 역시 증대되고 있는 것이다.

공간적 상호작용 데이터의 방법론적 진보를 꾀하기 위해서는 우선 공간적 상호작용 데이터의 특수성을 보다 정교하게 인식할 필요가 있다. 공간적 상호작용 데이터의 특수성은 다음의 세 가지 측면으로 살펴볼 수 있다(이상일, 2012). 첫째, 공간데이터분석의 측면에서, 공간적 상호작용 데이터는 ‘측정지(地)-측정치(値) 모형’이라고 하는 기본적인 데이터 구조를 따르지 않는다. 단일 측정지가 아니라 측정지의 쌍으로 구성되며, 측정치는 ‘개별적’ 속성이 아니라 ‘관계적’ 속성이다. 이는 통계학적 모델링이나 공간적 자기상관 연구에서 다양한 형태의 제약을 부과한다(Black, 1992; Baily and Gatrell, 1996; Chun, 2008; LeSage and Pace, 2008). 둘째, GIS의 측면에서, 공간적 상호작용 데이터는 GIS의 기본적 재현 유형(포인트, 라인, 폴리곤) 중 그 어느 것에도 정확히 부합하지 않는다. 속성 데이터는 명확히 존재하지만 기하 데이터는 본질적으로 모호하다. 이로 인해 두 포인트를 연결하는 라인 개체를 대체물로 사용할 수밖에 없고, GIS 데이터베이스는 두 개의 인덱스 필드를 요구할 수밖에 없다(김감영･이상일, 2012; Kim et al., 2012). 셋째, 시각화의 측면에서, 공간적 상호작용은 시각혼란증(visual cluttering) 문제의 야기와 지도학적 표현의 다중성이라는 특성을 갖는다(김감영･이상일, 2012; Kim et al., 2012). 전자는, 특히 유선도의 경우, 항상 제한적 시각화만 가능하다는 측면을 지적하는 것이고, 후자는 유선도뿐만 아니라 도형표현도, 단계구분도 등의 다양한 방식으로 시각화될 수 있다는 측면을 지적하는 것이다.

인구이동, 특히 국내 인구이동(internal migration)은 통근(commuting)과 함께 가장 중요한 공간적 상호작용 현상들 중 하나로 인식되어 왔다(Stillwell et al., 2010). 인구이동은 전통적으로 국가 주도의 공공 데이터 구축에서 매우 중요한 부분을 담당해 왔다. 인구이동은 센서스의 주요 항목일 뿐만 아니라 행정 등록 정보의 중요한 부분을 차지한다. 그런데, 최근 국제 인구이동에 대한 학계의 열렬한 관심을 염두에 둔다면, 상대적으로 전통적이고 정체된 연구 분야로 비춰지고 있는 것도 사실이다. 그러나 국내 인구이동은 여전히 ‘인구이동 시대(age of migration)’ (De Haas et al., 2020)의 중요한 구성 요소이며, ‘새로운 모빌리티 패러다임(new mobilities paradigm)’ (Sheller and Urry, 2006)을 견인하고 있으며(Smith et al., 2015), 새로운 시각과 방법론을 끊임없이 요구하는 역동적이고 흥미로운 연구 영역으로 남아 있다(Champion et al., 2018). 인구이동 데이터의 특수성을 감안한 수많은 연구 방법론이 개발되고 적용되어 왔다(Stillwell et al., 2010; 이상일, 2012). 특히 데이터의 시간적 일관성의 문제(Duke-Williams and Stillwell, 2010), 인구이동과 ‘공간단위 임의성의 문제(modifiable areal unit problem, MAUP)’ (Stillwell et al., 2018; 김감영, 2011), 인구이동에서의 공간적 자기상관 연구(Chun, 2008; LeSage and Pace, 2008; 김영호, 2010) 등에서는 많은 방법론적 진보가 있었다.

본 연구는 인구이동 연구가 매우 기본적인 측면에서조차 여전히 해결되지 못한 많은 방법론적 문제를 내포하고 있다는 문제의식에 기반한다. 특히, 인구이동 양상을 다양한 인구 집단별로 세분화하여 다루고자 할 때 이러한 이슈는 보다 더 크게 부각된다. 첫째, 인구이동 양상을 O-D (origin-destination) 매트릭스로 재현하는 것의 한계점에 대해 보다 명확하게 인식할 필요가 있다. O-D 매트릭스는 기본적으로 ‘일변량적(univariate)’이며, 인구 집단별 인구이동을 다루기 위해서는 집단의 수만큼의 매트릭스를 생성해야 하는데, 그것을 통합적으로 다루는 방법론은 제한적일 수밖에 없다. 둘째, 인구이동 플로(flow)라고 하는 카운트(count) 데이터를 어떻게 표준화할 것인가가 매우 중요한 사안이라는 점을 보다 명확히 이해해야 한다. 인구이동 플로는 본질적으로 이산적인, ‘공간적으로 외연적인(spatially extensive)’ 속성이며, 많은 통계학적 이슈를 내포하고 있다(조대헌, 2013). 셋째, 진정한 다변량 분석 기법의 적용 방안을 모색해야 한다. 대표적인 다변량 분석 기법 중 하나인 주성분분석(principal component analysis, PCA)이 인구이동 연구에 활발하게 적용되어 왔지만(Demšar et al., 2013), 그것은 앞에서 언급한 ‘일변량’ O-D 매트릭스에 출발지와 도착지 중 하나를 변수로 취급한, 매우 제한적인 방식의 것이었고, 통계학적으로도 완전히 해소되지 못한 다양한 문제점을 보유하고 있는 것으로 지적되어 왔다(조대헌, 2011).

이러한 측면에서, 본 논문의 주된 연구 목적은 인구이동 플로의 하위 집단별 특화도 패턴 분석을 위한 하나의 방법론적 대안을 제안하는 것이다. 특히 인구이동 플로가 연령 집단별로 어떠한 차별적인 특성을 드러내는지를 정량적으로 분석할 수 있는 방법론의 개발에 초점을 맞추고자 한다. 이를 위해 우선 O-D 매트릭스에 대한 대안으로서 다이아딕(dyadic) 매트릭스의 장점을 강조하고자 한다. 다이아딕 매트릭스는 ‘방향적 지역쌍(directional region pair)’별 데이터를 구축하는 방식으로 하위 집단별 인구이동 양상을 다변량 데이터셋으로 나타낼 수 있는 장점이 있다. 인구 집단별 인구이동 플로를 표준화하는 방법으로서 표준화상이점수(standardized score of dissimilarity, SSD)의 유용성에 주목할 것이다(이상일, 2008; 조대헌, 2013). SSD는 상이지수(index of dissimilarity)의 국지적 버전으로 이해할 수 있는데, 해당 카운트 변수를 준거 카운트 변수에 의거하여 일종의 표준점수(z-score)의 형식으로 표준화한 것으로, 하위 집단별 인구이동의 특화도를 표현하는 유용한 기법이 될 것으로 기대된다. 마지막으로 SSD로 표준화된 하위 집단별 인구이동 양상을 PCA의 프레임 속에 넣어 진정한 다변량 분석의 전형을 제시하고자 한다. 이러한 총체적인 연구 프레임의 적용성을 평가하기 위해 2020년 우리나라 시군구 단위 인구이동 데이터의 분석에 적용하고자 한다.

2. 인구이동 플로의 연령-특수적 패턴 분석을 위한 방법론의 확립

1) 다이아딕 매트릭스

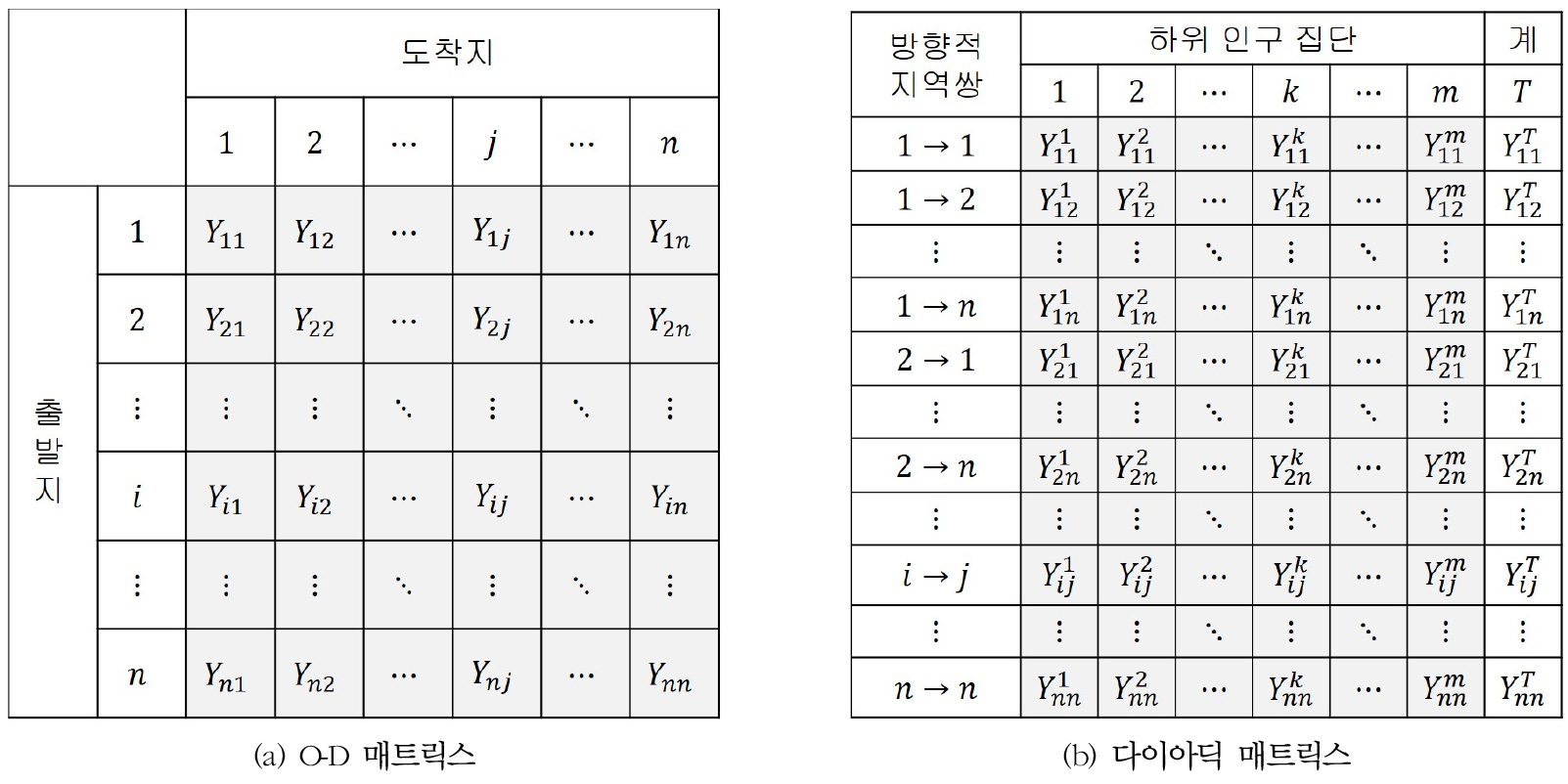
이론적인 의미에서 가장 복잡한 공간적 상호작용 데이터는 무한의 차원을 가질 수 있지만, 일반적인 의미에서는 ‘출발지-도착지-속성’이라고 하는 3차원 배열(array)로 이해할 수 있다(Davies and Thompson, 1980). 이 때 속성이란 공간적 상호작용의 종류 혹은 범주와 관련된 것으로 개수는 다양할 수 있다. 인구이동의 예를 들자면, 연간 인구이동 플로라고 하면 속성이 하나인 것이고, 인구이동 플로가 연령별로 세분화되어 있다면 그것은 속성이 여러 개인 것이다. 이러한 공간적 상호작용의 3차원 배열을 2차원으로 전환하는 방식이 크게 ‘O-D 매트릭스’ 방식과 ‘다이아딕 매트릭스’ 방식으로 나뉜다(Davies and Thompson, 1980; Yan and Thill, 2009). 그림 1은 이 두 가지 방식을 도해하고 있다.

O-D 매트릭스 방식(그림 1(a))은 n개의 지역간 인구이동 플로를 n×n 정사각행렬로 표현한 것으로, 속성이 한 개인 공간적 상호작용 데이터에 대한 완벽한 2차원 재현이다. 지역내 인구이동을 고려하지 않는다면 주대각 요소는 모두 0으로 치환된다. 여러 하위 인구 집단을 고려하려면 하위 집단 개수만큼의 O-D 매트릭스가 필요하다. 이와 달리 여러 개의 속성을 2차원 매트릭스로 나타낸 것을 다이아딕 매트릭스라고 부른다(Black, 1973; Davies and Thompson, 1980). 그림 1(b)에 나타나 있는 것처럼, 이 매트릭스는 ‘방향적 지역쌍(출발지 → 도착지)’을 다수의 플로 속성과 결합한 것인데, n2×m 매트릭스로 나타난다. 지역내 이동을 고려하지 않는다면 다이아딕 매트릭스의 크기는 n(n-1)×m으로 축소된다. 다이아딕 매트릭스의 속성이 다양한 연령 집단을 나타낸 것이라면 m은 연령 혹은 연령층의 개수가 된다. 행렬의 맨 오른쪽에 있는 전연령 인구이동 플로는 연령별 속성의 합산을 통해 생성될 수도 있고, 처음부터 하나의 속성으로 투입될 수도 있다. 그런데 다이아딕 매트릭스의 속성이 반드시 하위 인구 집단이어야 하는 이유는 없다. 인구이동 데이터를 다이아딕 매트릭스로 정렬하는 또 다른 방식에 전체 인구이동 플로에 초점을 맞추고 속성으로 연도로 사용하는 것이 있을 수 있다(Elmes and Harris, 1996). 속성의 준거가 연령 집단이건 시점이건 모두 인구이동 데이터를 다이아딕 매트릭스로 구성하는 동일한 원리에 입각하고 있는 것이다.

O-D 매트릭스에 비해 다이아딕 매트릭스를 활용한 연구의 양은 비교가 안될 정도로 적다. 다이아딕 매트릭스의 보다 적극적인 활용이 필요하다고 판단하며 여기에 두 가지 논지를 제시하고자 한다. 첫째, O-D 매트릭스는 기본적으로 일변량적이라는 한계가 있으며, 공간적 상호작용 데이터에 대한 보다 완전한 다변량 통계 분석의 길로 나아가기 위해서는 다이아딕 매트릭스의 활용이 필수적이다. 둘째, O-D 매트릭스는 기본적으로 지역간 혹은 지역별 분석으로 한정되지만, 다이아딕 매트릭스는 지역쌍별 혹은 지역쌍간 분석으로 확장될 수 있다. O-D 매트릭스를 통해 단일 속성의 지역간 상호작용 플로를 파악할 수 있고, 행별 혹은 열별 합산을 통해 손쉽게 지역별 데이터로 전환할 수도 있다. 다이아딕 매트릭스는 이러한 O-D 매트릭스의 특성을 모두 포괄한다. 실질적으로 하나의 O-D 매트릭스는 다이아딕 매트릭스의 한 열을 의미한다. 지역간 데이터로의 전환도 방향적 지역쌍의 이중 인덱싱을 통해 손쉽게 구현될 수 있다. 무엇보다도 다양한 공간적 상호작용 속성을 매트릭스의 열에 무한 확장할 수 있다는 점이 가장 중요한 이점이다.

2) 인구이동 플로의 표준화

인구이동 플로는 이산적인 카운트 데이터이므로 정규분포를 가정한 표준화 기법을 사용할 수 없고, 통상적으로 사용되는 공간적 자기상관 통계량도 적용할 수 없다(Oden, 1995; Tango, 1995; Rogerson, 1999). 발병 빈도를 다루는 보건통계학이나 의료지리학에서는 이러한 카운트 데이터를 표준화하는 기법의 개발에 많은 힘을 쏟아왔다(Waller and Gotway, 2004; Rogerson and Yamada, 2009). 여기서는 이상일(2007; 2008)이 제안한 ‘표준화상이점수(standardized score of dissimilation, SSD)’의 활용을 제안하고자 한다. SSD는 이름에도 나타나 있는 것처럼, 일반적으로 흔히 사용되는 표준점수(z-scores)와 거주지 분리 연구에서 널리 사용되는 상이지수(index of dissimilation)를 결합한 것이다. 두 행-비중(column proportions)의 차로 정의되는 상이지수의 기본 공리를 이용하되 표준점수의 국지적 통계량으로서의 특징과 0을 중심으로부터 양 방향으로 멀어질수록 특이성이 증가하는 특성을 그대로 이어받은 것이다.

SSD의 기본 공식은 다음과 같이 주어진다(이상일, 2008; 이화정 등, 2013).

여기서 ri는 첫 번째 변수(혹은 관심 변수)에 대한 i번째 공간단위의 열-비중이고, pi는 두 번째 변수(혹은 준거 변수)에 대한 i번째 공간단위의 열-비중이다. Xi는 i번째 공간단위의 첫 번째 변수(혹은 관심 변수) 값, X는 모든 공간단위의 첫 번째 변수(혹은 관심 변수) 값의 합, Yi는 i번째 공간단위의 두 번째 변수(혹은 준거 변수) 값, Y는 모든 공간단위의 두 번째 변수(혹은 준거 변수) 값의 합이다. SSD의 평균은 0이고, 표준편차는 1이며, 따라서 2보다 크거나 -2보다 작다면 대략 통계적으로 유의한 만큼 크거나 작다고 해석할 수 있다(이상일, 2008; 이화정 등, 2013). 이 표준화 기법은 공간적 상호작용 데이터가 아닌 일반적인 개체-변수 형태 혹은 측정지-측정치 형태의 데이터에 적용되어 그 유용성이 인정된 바 있다(이상일, 2008; 이화정 등, 2013; 이남승, 2016; 전창우, 2017; 주뢰, 2019; 이소영, 2020; 박지희, 2021).

이제 중요한 것은 이 표준화 기법을 공간적 상호작용 데이터에 적용하기 위해 확장하는 것이다. 그림 1(b)의 다이아딕 매트릭스에서 k번째 인구 코호트의 인구이동 플로를 마지막 열에 있는 전연령 합산 플로를 준거로 삼아 표준화하는 경우를 상정해 보자. 그러면 식 (1)은 다음과 같이 변형되는데, 이것을 ‘플로 SSD’라고 부르고자 한다.

여기서 SSDij는 i→j쌍의 플로 SSD, Yijk는 k번째 연령 집단의 i→j 인구이동 플로, ∑Yijk은 k번째 연령 집단의 총 인구이동 플로(다아아딕 매트릭스의 k번째 열의 합산값), YijT는 전연령의 i→j 인구이동 플로, ∑YijT는 전연령의 총 인구이동 플로(다아아딕 매트릭스의 T열의 합산값)이다.

이는 방향적 지역쌍별 k번째 연령 집단의 플로 특화도를 계산해 준다고 할 수 있다. 즉, 플로 SSD의 값이 크다는 것은 해당 i→j쌍의 비중이 해당 연령에서 상대적으로 높다는 것을 의미한다. 좀 더 자세히 설명하면 다음과 같다. 우선 전연령에 대한 인구이동 플로의 크기는 지역쌍에 따라 다양하게 나타날 것이다. 이러한 다양성은 기본적으로 출발지와 도착지의 인구 규모, 그리고 공간적 분리도에 의해 결정된다(Haynes and Fotheringham, 1984; Fotheringham and O’Kelly, 1989). 그림 1의 다이아딕 매트릭스의 가장 오른쪽 열에 대해 열-비중을 구한다면, 그 값은 특정 지역쌍의 인구이동 플로가 전체 인구이동 플로에서 차지하는 비중이 된다. 그런데 인구이동에서 특정 연령 집단이 아무런 차이를 만들지 않는다면, 즉 해당 연령 집단의 인구이동 양상이 전체 인구의 인구이동 양상과 동일하다면, 그림 1(b)의 k번째 연령 집단의 열에 대한 열-비중 값은 전체 인구이동 플로의 열-비중 값과 동일하게 나타날 것이다. 그런데 어떤 지역쌍이 특정 연령 집단에서 전체 인구에 대한 열-비중보다 더 높은 열-비중을 보인다면 그 지역쌍은 해당 연령 집단의 인구이동에 특화되어 있다고 말할 수 있을 것이다.

그림 1.

공간적 상호작용 데이터를 2차원 매트릭스로 정렬하는 두 가지 방식

플로 SSD의 작동성을 평가하기 위해 입지계수(location quotient, LQ) 개념에 기반한 다른 측도와 비교해 보고자 한다. 연령별 인구이동의 특화도를 위한 입지계수는 다음과 같은 공식을 통해 산출될 수 있고 이를 ‘플로 LQ’라고 부르고자 한다.

식 (3)을 자세히 살펴보면, 식 (2)의 분자 부분에 대해 차를 구하는 대신 비를 구하고 있다는 사실을 알 수 있다. 통상적인 LQ에 대한 해석과 마찬가지로, 플로 LQ가 1보다 크면 특정 지역쌍이 해당 연령 집단의 인구이동에 특화되어 있다고 말할 수 있다. 플로 SSD는 플로 LQ에 비해 다음의 세 가지 점에서 우위에 있다. 첫째, 특정 i→j쌍에 해당 연령 집단은 물론 전인구에 대해서도 인구이동 플로가 0이라면, 식 (3)은 아무런 값도 산출할 수 없다. 하지만 동일한 경우 SSD는 합리적인 값, 0을 산출한다. 둘째, 플로 SSD는 플로 LQ와 달리 플로의 절대적 규모를 감안한다. 즉, 동일한 플로 LQ를 보이는 경우라 하더라도 전체적인 인구이동 규모가 크다면 더 큰 값을 산출한다. 따라서 SSD는 단순한 특화도라기 보다는 ‘규모를 감안한 특화도’의 측도라고 말할 수 있다. 셋째, 통계적인 유의성에 대한 일반 원리를 원용하여 적용할 수 있다. 즉, 플로 SSD의 값이 2보다 크면 통계적으로 유의한만큼 특화되어 있다고 해석할 수 있다. 그러나 플로 LQ에 대해서는 이러한 방식으로 해석할 어떠한 근거도 존재하지 않는다.

3) 다이아딕 PCA의 가능성

공간적 상호작용 혹은 인구이동 데이터에 대해 다양한 다변량 통계 분석 기법이 적용되어 왔지만 가장 널리 사용된 것은 PCA일 것이다(Demšar et al., 2013). 대부분의 연구는 그림 1(a)의 기본적인 O-D 매트릭스에 PCA를 적용하는 것이다. 이 때 행이 출발지, 열이 도착지인 경우를 R-모드라고 하며, 반대로 행이 도착지, 열이 출발지인 경우를 Q-모드라 부른다(Clayton, 1977). R-모드 분석은 도착지로서의 특성(인플로(in-flow)의 지역 구성)이 유사한 지역들을 묶어 그것을 대변하는 몇 개의 가상의 도착지를 구성하고자 하며, Q-모드 분석은 이와는 반대로 출발지로서의 특성(아웃플로(out-flow)의 지역 구성)이 유사한 지역들을 묶어 그것을 대변하는 몇 개의 가상의 출발지를 구성하고자 한다.

R-모드를 중심으로 좀 더 자세히 살펴보면 다음과 같다. 각 열을 표준점수로 전환하는 것이므로 O-D 매트릭스에 열-표준화(column-standardization)을 적용하는 것과 동일하다. PCA 결과 도출되는 PC 적재량(loadings)은 도착지로서 각 지역이 가상의 PC와 얼마나 유사한가를 보여주는데, 높은 값을 보인 지역들은 해당 PC와 유사성이 높으면서 서로서로 유사하다는 것을 의미한다. PC 점수는 출발지로서 각 지역이 가상의 PC와 얼마나 관련되어 있는 가를 보여주는데, 높은 값을 보인 지역들은 그 PC(PC 적재량에서 높은 값을 보인 지역들)로 주된 플로를 제공한다는 것을 의미한다. 이것을 이용하면 공간적 상호작용의 응집성이 현저히 드러나는 기능 지역을 구성할 수 있다. 즉, 각 PC에 대해 최대 PC 점수를 보이는 지역(출발지, 1개)을 선정하고, 그것과 해당 PC에서 최대 적재량을 보이는 지역(도착지, 다수 가능)을 연결하여 유선도 혹은 정성적 주제도 형식으로 표현할 수 있다(Clayton, 1977; Pandit, 1994; 권상철, 2009).

그러나 가장 널리 사용되는 방법은, 각 PC에 대해, 특정한 값 이상의 PC 점수를 보인 지역(출발지, 다수 가능)과 특정한 값 이상의 PC 적재량을 보인 지역(도착지, 다수 가능)을 선으로 연결하여 복잡한 네트워크 형태로 표현하는 것이다(Goddard, 1970; Clayton, 1977; 손승호, 2007; 이경선, 2007). 네트워크 표현을 단순화하기 위해 원 매트릭스에서 흐름량이 상대적으로 많은(예: 상위 10%) 플로만 표현하는 방법이 채택된다. 마지막 방법은 일종의 국지적 분석으로 지역별 인구이동장(migration field)을 표현하는 것이다(Pandit, 1994). 각 PC에 대해, 최대 PC 점수를 보인 지역(출발지, 1개)과 특정한 값 이상의 PC 적재량을 보인 지역(도착지, 다수 가능)을 선정하여 지도에 표시할 수 있는데, 특정 출발지의 아웃플로 필드를 나타낼 수 있다.

다이아딕 매트릭스에 PCA를 적용한 연구(다이아딕 PCA)는 O-D 매트릭스에 PCA를 적용한 연구(O-D PCA)에 비해 현저히 작다. 다이아딕 PCA는 Black(1973)의 선구적인 연구에 의해 시작되었다. 그는 24개 상품의 9개 센서스 지역간 플로에 대해 다이아딕 PCA를 실시하여 5개의 주요 PC를 추출하고, 개별 PC에 대해 높은 PC 점수를 보인 지역쌍을 지도에 표시하였다. 뒤 이은 연구들은 이 연구의 프레임을 그대로 답습하였는데, 예를 들어 Davies and Thompson(1980)은 17개 시도간 15개 상품의 유동량에 대해 다이아딕 PCA를 적용했다. 그러나 다른 다이아딕 PCA의 기본 프레임을 시계열 분석에 사용한 경우도 있었다. Elmes and Harris(1996)은 주간 석탄 유동량을 대상으로 1972~1990의 19개 연도를 변수로 하여 다이아딕 PCA를 적용하고, 해당 시계열 경향을 가장 잘 대변하는 지역쌍을 시각화하였다.

O-D PCA와 다이아딕 PCA를 비교할 때 후자의 연구가 보다 활성화되어야 할 충분한 이유가 있다. 첫째, O-D PCA는 방법론적으로 흠결이 많다. 가장 중요한 것은 R-모드의 경우 도착지, Q-모드의 경우 출발지는 관측개체일 뿐 ‘변수’가 아니다. 이것은 데이터 큐브(data cube)로부터 6개의 서로 다른 모드가 가능하다고 주장한 Rummel(1970)의 논리를 너무 무비판적으로 수용한 결과일지도 모른다. 둘째, O-D 매트릭스의 주대각 요소의 값이 PCA 결과 해석을 매우 어렵게 한다. 지역내 이동을 고려하지 않는 경우는 0이 모든 주대각 요소에 놓이고, 지역내 이동을 고려하는 경우는 매우 큰 값이 주대각 요소에 놓이게 된다. 이것은 PCA 투입시 표준화 과정에서 매우 작은 혹은 매우 큰 극단값이 되기 때문에 PCA 결과에 큰 영향을 끼친다. 셋째, O-D PCA는 기본적으로 일변량 분석이다. 이는 일변량 데이터를 다변량 기법에 투입한 것이나 마찬가지이다. 일변량 분석을 여러 번 행할 수 있지만, 일련의 일변량 분석이 한 번의 다변량 분석을 대체할 수는 없다. 다이아딕 매트릭스의 행에 다양한 변수를 투입함으로써 진정한 인구이동 데이터에 대한 다변량 분석의 길로 나아가야 한다.

마지막으로 기존의 다이아딕 PCA에 본 연구가 기여하는 점에 대해 설명하고자 한다. O-D PCA와 기존의 다이아딕 PCA가 공통적으로 가지고 있는 단점은 카운트 데이터를 막바로 PCA의 프레임 속에 투입한다는 점이다. PCA의 기본적인 표준화 과정뿐만 아니라 공분산 혹은 상관계수 산출 절차 모두 카운트 데이터의 속성에 부합하지 않는다. 본 연구는 식 (2)에 나타나 있는 플로 SSD를 PCA의 원 변수로 투입함으로써 이러한 문제점에 대한 하나의 해결책을 제시하고자 하며, 보다 합리적인 PCA의 결과가 도출될 것으로 기대한다.

3. 2020년 우리나라 인구이동 양상의 분석

1) 다이아딕 매트릭스의 구축

본 연구의 데이터는 통계청의 2020년 ‘국내인구이동통계’이다. 2020년 한 해 동안 읍면동 수준에서는 총 7,735,491명(이동률: 15.1%), 시군구 수준에서는 4,809,085명(이동률: 9.4%), 시도 수준에서는 2,534,114명(이동률, 4.9%)이 이동했다(통계청, 2021)¹⁾. 그런데 본 연구에서는 변형된 시군구 수준의 공간단위 체제를 사용하고자 한다. 이 변형된 공간단위 수준을 ‘시군 수준’이라고 명명하고자 하는데, 일반적으로 사용되고 있는 시군구 수준에서, 특별시 및 광역시의 자치구의 경계를 없애고, 특별시 및 광역시 자체가 나머지 시군과 동등하게 취급되게 하는 것이다. 이렇게 하면 229개 시군구 단위가 162개의 시군 단위로 축소된다. 이렇게 하는 가장 중요한 이유는 인구이동의 경향성 파악에 일반적인 시군구 단위보다 이 시군 단위가 보다 유리한 측면이 있기 때문이다(시군 단위의 정의와 그것의 사용에 대한 정당화는 이상일･이소영, 2019 참조).

162개 시군을 공간단위로 사용할 경우, 2020년 한 해 동안 이 시군 경계를 넘어 인구이동을 실행한 인구는 총 3,502,779명(이동률: 6.8%)이다. 지역내 이동을 감안하지 않았으므로 총 26,082개(162×161)의 방향적 지역쌍이 가능하다. 이것을 바탕으로 그림 1(b)에 나타나 있는 것과 같은 다이아딕 매트릭스를 구성하였다. 실질적인 변수 역할을 하는 하위 인구는 5세 간격의 연령 집단이다. ‘0~4세’에서 ‘80세 이상’에 이르는 총 17개의 연령 집단별 인구이동 플로를 기본 변수로 삼았으며, 여기에 그림 1(b)의 맨 끝에 있는 전연령 인구이동 플로도 따로 포함시켜 총 18개의 변수로 구성하였다. 성도 함께 고려하여 하위 인구를 정의한다면 전연령 인구이동량을 포함하여 총 35개 변수가 생성될 것이다. 결국 본 연구에서 사용된 데이터셋은 26,082×18 크기의 다이아딕 매트릭스이다.

총 26,082쌍 중 1.1%에 해당하는 2,908개의 지역쌍에는 인구이동 플로가 전혀 없으며, 전연령 인구이동 플로가 10명 이하인 경우도 절반을 넘는 13,283개에 달한다. 그리고 1,000명 이상의 전연령 인구이동 플로를 기록한 지역쌍은 563개에 불과하다. 전연령 인구이동 플로에서 가장 큰 값을 보인 방향적 지역쌍은 서울 → 경기 고양시(43,439명), 서울 → 인천(39,875명), 인천 → 서울(38,409명), 서울 → 경기 남양주시(29,799명), 서울 → 김포시(29,480명) 등으로 주로 서울로부터 서울 주변의 인천과 경기도 시 지역을 향한 플로이다²⁾.

2) 인구이동 플로의 표준화

식 (2)에 규정되어 있는 플로 SSD를 활용하여 17개 인구 코호트 변수의 표준화를 실시하였다. 비교를 위해 식 (3)에 나타나 있는 플로 LQ도 함께 산출하였다. 예를 위해 연령 계급별로 이동자수가 가장 많고 이동률도 가장 높은 25~29세 연령 집단을 선정하였다. 2020년의 25~29세 이동자수는 1,014천 명(이동률: 28.9%)이었으며, 그 뒤를 이어 30~34세가 847천 명(이동률: 27.0%)을 기록했다(통계청, 2021).

표 1에는 플로 SSD와 플로 LQ에 의거해 상위 10개에 해당되는 지역쌍과 해당 표준화 값, 그리고 25~29세 이동자수가 나타나 있다. 우선 플로 SSD의 표준화 결과를 살펴보면 다음과 같다. 대부분 특별･광역시와 경기도의 대도시 간 지역쌍이 극단적으로 높은 값을 나타냈다. 이것은 앞에서 말한 것처럼 SSD는 규모를 고려한 표준화 지표이기 때문에 나타나는 당연한 결과이다. 그러나 그럼에도 불구하고 이동 규모가 크다고 해서 반드시 SSD도 높게 나타나는 것은 아니라는 점을 명확히 이해할 필요가 있다. 1위와 2위를 차지한 경우를 사례로 들어 설명하고자 한다. 이동자수가 가장 많은 것은 8,024명을 기록한 인천 → 서울이고, 플로 SSD에서 1위를 기록한 부산 → 서울의 5,475명은 13위에 해당하는 규모이다. 그러나 SSD의 값은 오히려 후자가 조금 더 높다. 이러한 결과가 나타난 것은, 인천 → 서울의 경우 준거가 되는 전연령 이동자수가 38,409명으로 전체 3위를 할 만큼 큰데 반해, 부산 → 서울의 경우는 전연령 이동자수가 20,990명으로 전체 13위를 기록했다. 즉, 전연령 이동자수로 비교하면 인천 → 서울이 부산 → 서울에 비해 거의 2배에 달하지만 25~29세의 경우는 1.5배 정도에 불과하다. 따라서 부산 → 서울이 인천 → 서울에 비해 이동자수는 적음에도 불구하고 해당 연령층에서는 더 높은 특화도를 보인 것이다.

이와는 대조적으로 플로 LQ에서 가장 높은 값을 보인 곳은 모두 이동자수가 매우 작은 지역쌍이다. 여기에 나타난 10개 지역쌍은 전연령 이동자수와 25~29세 이동자수가 동일한 경우이다. 식 (3)에 이 사실을 대입해 보면, 결국 플로 LQ 값은 총 전연령 이동자수(3,502,779명)를 총 25~29세 이동자수(526,124명)로 나눈 것으로 그 값이 바로 6.658인 것이다. 이러한 지역쌍이 모두 389개에 이른다. 앞에서 언급한, 인구이동 플로가 전혀 없는 2,908개의 지역쌍에 대해서는 아예 플로 LQ가 산출되지 않는다. 플로 LQ로 상위 10개에 해당되는 지역의 플로 SSD 값은, 1위는 0.099, 2~5위는 0.079, 나머지 6~10위는 0.059인데, 모두 0에 근접한 값으로 이동자수를 고려할 때 매우 합리적인 값이 도출된 것으로 평가할 수 있다. 따라서 플로 SSD는 플로 LQ에 비해 최소한 연령별 특화도 계산이라는 측면에서 우위에 있다.

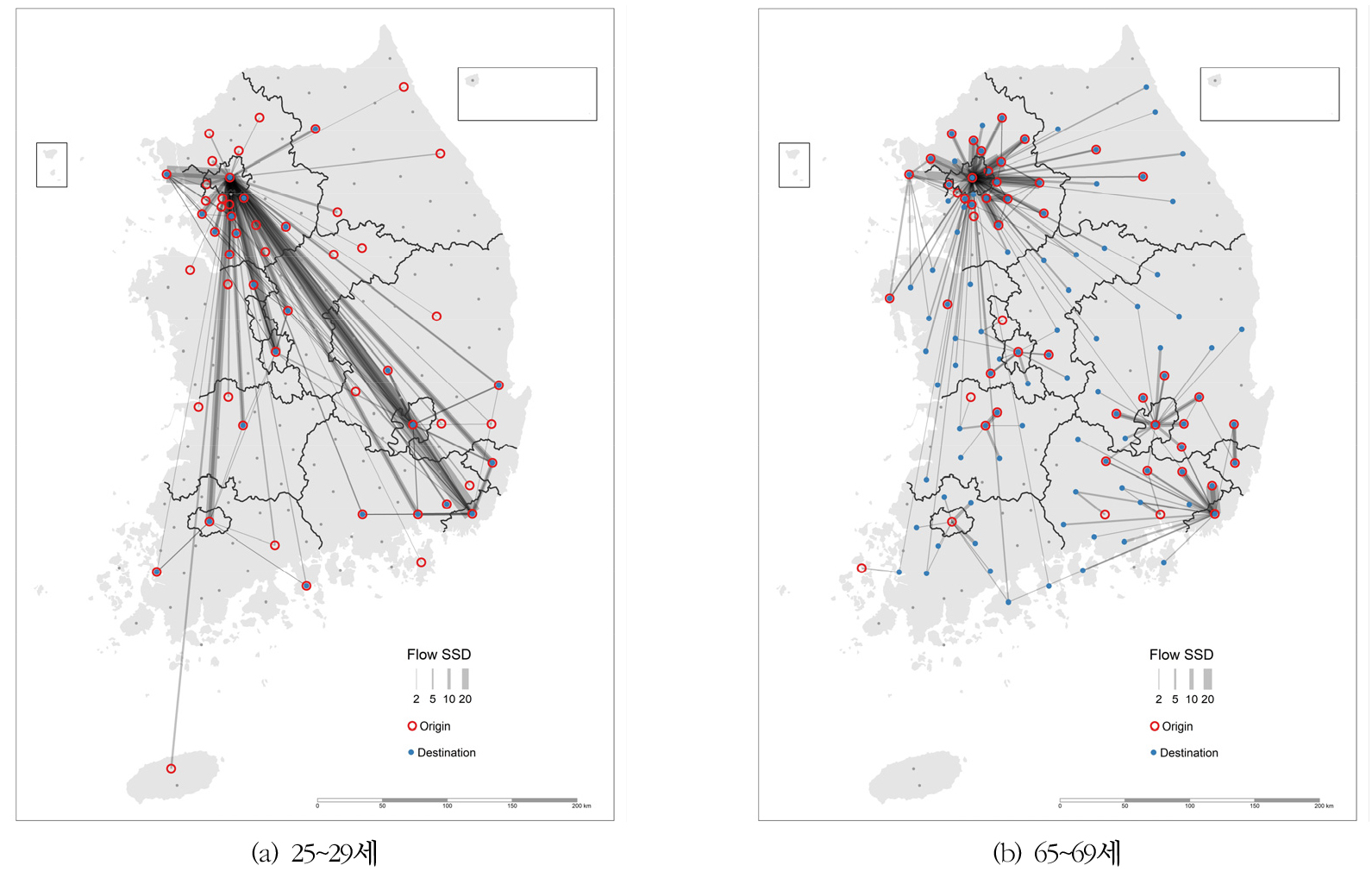
플로 SSD에 의한 인구 집단별 특화도의 유용성을 좀 더 면밀히 검토하기 위해, 두 개의 연령 집단(25~29세와 65~69세)에 대해 플로 SSD 값이 2보다 큰 플로를 시각화하였다(그림 2). 이 두 연령 집단을 선택한 것은, 둘 다 중요한 생애 주기 단계를 대변할 뿐만 아니라, 대조적인 패턴을 보일 것이 기대되었기 때문이다. 그림 2(a)에 나타나 있는 25~29세의 경우, 서울 일극 지향성이 현저하다. 플로 SSD가 20이 넘는, 극단적인 특화도를 보인 플로가 부산, 인천, 대구, 경기 수원, 대전, 광주에서 서울로 향하는 플로이다. 그림 2(b)의 65~69세의 경우는 앞의 지도와는 전혀 다른 패턴을 보여주고 있다. 즉, 대도시로부터의 이심화가 두드러진다. 물론 이동 규모로 인해 극단적으로 높은 값은 주로 수도권 내에서 나타나고는 있지만 플로 SSD 2 이상을 보이는 플로의 도착지가 전국적으로 펼쳐져 있음에서 알 수 있듯이, 특화도의 측면에서, 은퇴자의 흐름은 젊은 층의 흐름과는 완전히 구별된다.

그림 2.

연령 집단별 플로 SSD의 분포 패턴

3) 플로 SSD를 이용한 다이아딕 PCA의 실행

위에서 산출된 연령 집단별 플로 SSD를 이용해 다이아딕 PCA를 수행하고자 한다. 이렇게 하는 가장 중요한 이유는, 어떤 연령층들은 특화도에서 유사한 패턴을 보일 것으로 기대되고, 따라서 개별 17개 연령층별 특화도 패턴을 살펴보는 대신, 몇 개의 특화도 차원을 추출하여 그것을 중심으로 설명하는 것이 더 효율적이기 때문이다. 예를 들어, 15세 미만은 그들의 부모 연령층의 특화도와 유사한 패턴을 보일 것이 확실하고, 인접한 연령층은 그렇지 않은 연령층에 비해 유사성이 높을 가능성이 훨씬 더 높다. 예를 들어 그림 2에서 살펴본 25~29세는 20~24세와, 65~69세는 70세 이상과 유사할 가능성이 높다. 플로 SSD를 투입 변수로 PCA를 수행하는 것의 상대적인 강점을 논증하기 위해 원 플로 데이터와 플로 LQ를 투입 변수로 PCA를 수행한 것의 결과와 비교하였다.

우선 원 이동량을 투입한 PCA의 결과를 보면, PCA가 아무런 의미가 없음을 알 수 있다. 모든 연령층이 PC1과 극단적으로 높은 적재값을 보여주고 있고, 해당 PC의 고유값이 15.825로 17개 변수의 93.1%를 설명하고 있다. 이러한 결과가 나타난 것은 당연한 것이다. 어떤 연령층이건 이동량 자체는 출발지와 도착지의 인구 규모와 밀접히 관련되어 있기 때문에 이동량의 플로간 변동은 연령층별로 큰 차이를 보일 수가 없다. 즉, 연령층별로 절대적인 이동량에는 차이가 있겠지만 플로간 상대적인 비중 관계에는 큰 차이가 없다는 것이다. PCA 과정에서 우선적으로 변수를 표준화한다는 점을 염두에 둔다면 이러한 결과가 더 잘 이해될 것이다. 두 번째로 플로 LQ를 투입한 결과를 보면, 이것 역시 큰 의미가 없음을 알 수 있다. 특히 PC1의 고유값이 1.5 정도로 높지 않고, 나머지 3개의 PC 역시 1에 매우 근접해 있다. 상위 네 개의 PC가 17개 변수의 30.0%만을 설명할 뿐이다. 이러한 현상 역시 표 1에서 설명한 플로 LQ의 특징을 이해한다면 어렵지 않게 납득될 수 있다. 즉, 플로 LQ는 절대적인 플로 규모를 전혀 고려하지 않기 때문에, 매우 작은 이동량을 보이는 지역쌍에서 극단적인 특화도 값이 나타날 수 있고, 이것이 전체적인 분석 결과에 영향을 주어 특징적인 PC가 도출되는 것을 방해했을 것이다.

이에 비해, 플로 SSD를 투입한 PCA는 합리적인 결과를 도출하고 있다. PC1의 고유값은 5.445로 전체 변량의 32% 이상을 설명하고 있다. 또한 PC2~PC4의 고유값도 각각 4.999, 1.693, 1.370으로 이 네 개의 PC가 17개 변수의 총변동의 거의 80%를 설명하고 있다. PC5의 고유값이 0.693으로 매우 낮은 것을 염두에 두면, 이 네 개의 PC는 연령층별 인구이동의 특화도를 매우 요약적으로 보여주는 것이라 결론지을 수 있다. PC1은 30대 중후반에서 40대 중후반에 이르는 연령대와 그들의 자식 세대에 해당하는 0~14세 연령층이 높은 적재값을 나타내고 있다. 결혼과 자녀 출산에 따른 인구 이동 양상을 가장 잘 보여주는 PC라 할 수 있다. PC2에는 20대 초반에서 30대 초반에 이르는 연령층의 적재값이 가장 높게 나타나고 있는데, 가장 이동률이 높은 젊은 층의 인구 이동 양상을 대변하는 PC로 이해된다. PC3는 가장 해석하기 어려운 PC로 판단된다. 이미 PC1과 PC2에서 높은 적재값을 보인 30대에서 가장 높은 적재값이 나타난다. 그런데 이 30대가 60대와 연동을 하고 있다는 의미에서 PC1이나 PC2와는 차별화된다. PC4는 60대 후반 이후의 연령대에서 상대적으로 높은 적재값이 나타나고 있어 노년층의 인구 이동의 특성을 가장 잘 반영하는 PC인 것으로 판단된다.

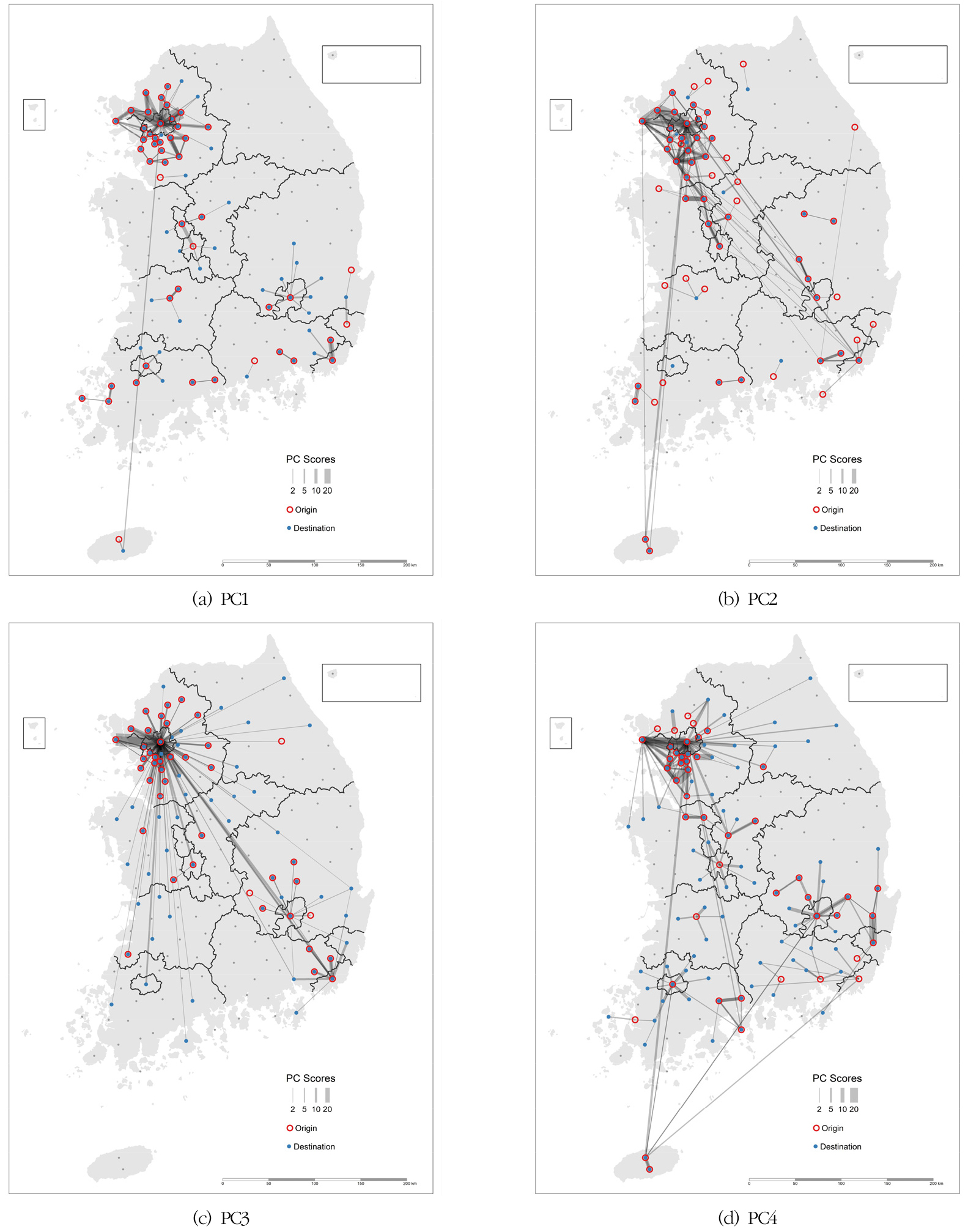
각 PC의 공간적 패턴 특성을 살펴보기 위해 앞의 플로 SSD를 시각화는 방식과 동일한 방식의 시각화를 시도하였다. 여기서는 시각화의 대상은 플로 SSD가 아니라 표준화 PC 점수이다. 그림 3(a)는 PC1의 분포를 보여주고 있는데, 각 권역별로 이심화가 두드러지게 나타나 있다. 이는 결혼 후 자녀가 중학교에 다니는 정도의 가정이 보여주는 특징적인 인구 이동 패턴을 잘 보여주는 것이다. 물론 이동 규모로 인해 수도권 내의 규모가 큰 도시 간의 이동이 가장 두드러진다. PC1에서 가장 높은 PC 점수를 보인 플로 중 5개가 서울에서 경기 남양주시, 고양시, 김포시, 의정부시, 파주시로 향하는 흐름이다. PC2의 분포를 보면, 그림 2(a)와 유사한 모습을 보이고 있는데, 주로 서울이나 수도권의 대도시를 향한 지향이 두드러지게 나타나 있다. 이는 젊의 층의 취업 관련 이동과 가장 관련이 깊은 것으로 해석된다. PC1과 마찬가지로 극단적으로 높은 특화도는 수도권 내에서 나타난다. PC1과 가장 큰 차이점은 PC1에서는 서울로부터의 이심화가 강했다면 PC2는 수도권 내 대도시간의 상호작용이 상대적으로 부각되어 나타난다는 점이다.

그림 3.

주성분별 PC 점수의 분포 패턴

PC3의 분포는 서울로부터 전국을 향한 이심화 현상을 모식적으로 보여주고 있는데, 그림 2(b)와 유사한 패턴이라고 볼 수 있다. 은퇴 직후 60대와 함께 거주 중인 30대의 동반 이동 양상을 가장 잘 보여주는 PC인 것으로 판단된다. PC1, PC2와 마찬가지로 극단적으로 높은 특화도를 보이는 플로는 수도권에 집중해 있다. 가장 높은 값을 보인 10개 지역쌍 중 무려 9개가 서울로부터 인천, 경기 고양시, 성남시, 수원시, 용인시, 부천시, 김포시, 화성시, 남양주시를 향하는 흐름이다. 서울로부터의 이심화의 종착지로서 수도권 외 지역으로는 부산, 대구, 대전, 충북 청주시, 충남 천안시, 광주 등이다. PC4는 70대 이상의 노년층의 이동 양상과 가장 깊은 관련성을 가지는 것으로 보인다. 그림 2(b)와 일부 유사하지만 보다 고령층의 이동 양상이 가미되어 다소 복잡한 패턴으로 나타난다. 수도권 내에서는 대도시 간 흐름이 복잡하게 얽혀 있고, 비수도권에서 특징적인 것으로는 울산 → 경북 경주시, 대구 → 경북 영천시, 대구 → 경북 성주군, 전남 광양시 → 전남 순천시, 충남 천안시 → 충남 아산시, 충북 청주시 → 충북 괴산군 등의 흐름이다.

4. 결론

본 논문의 주된 연구 목적은 인구이동 플로의 하위 집단별 패턴 분석을 위한 새로운 방법론을 제안하는 것이었다. 이 방법론을 구성하는 가장 중요한 요소로 세 가지 사항이 집중적으로 다루어 졌다. 우선 전통적인 O-D 매트릭스 대신 하위 인구 집단의 플로 속성이 변수로 다뤄질 수 있는 다이아딕 매트릭스의 적극적인 사용이 제안되었다. 둘째, 인구이동 플로를 표준화하는 측도로서 플로 SSD가 제안되었다. 플로 SSD는 개별 방향적 지역쌍에 대해 특정 연령 집단의 플로 특화도를 측정하는데, 특히 규모를 감안한 특화도를 산출해 준다는 측면에서 그 유용성이 큰 것으로 인정되었다. 셋째, 연령 집단별 인구이동의 플로 SSD 값을 변수로 투입한 PCA의 활용이 제안되었다.

이 분석 프레임워크의 적용성을 평가하기 위해 2020년 우리나라 시군구 단위 인구이동 데이터에 적용하여 분석하였다. 162개 시군 공간단위, 총 3,502,779명의 이동량, 총 17개의 연령 집단을 고려한 결과, 26,082×18 크기의 다이아딕 매트릭스가 구성되었다. 플로 SSD를 활용하여 17개 하위 인구 변수의 표준화를 실시하였는데, 이동 규모를 고려한 특화도 측정이라는 플로 SSD의 특성이 잘 드러났다. 두 개의 대표적인 연령 집단(25~29세와 65~69세)에 대해 플로 SSD 값이 2보다 큰 플로를 시각화한 결과, 전자에서는 서울을 향한 집중화 경향이, 후자에서는 서울로부터의 이심화 경향이 두드러지게 나타났다. 플로 SSD로 표준화된 변수를 PCA에 투입한 결과, 원 이동량과 플로 LQ를 투입한 PCA에 비해 훨씬 더 합리적인 결과가 도출되었다. 네 개의 PC가 총변동의 거의 80%를 설명하는 것으로 드러났다. PC1은 결혼과 자녀 출산에 따른 인구이동 양상을, PC2는 20대 초반에서 30대 초반에 이르는 연령층의 인구이동 양상을, PC3은 30대가 60대가 연동하는 인구이동 양상을, PC4는 60대 후반 이후 연령대에서의 인구이동 양상을 대변하는 것으로 해석되었다. 각 PC별로 높은 PC 점수를 보이는 플로를 시각화한 결과 PC별로 특징적인 공간적 패턴이 드러났다. 결과적으로 말해, 본 연구에서 제안된 방법론은 인구이동 플로의 연령-특수적 패턴을 분석하는데 매우 유용한 것으로 평가되었다.

본 연구는 다양한 방식으로 확장될 수 있다는 측면에서 의의가 있다. 가장 중요한 확장성은 다이아딕 매트릭스의 확장성이다. 본 연구의 사례는 특정 연도의 서로 다른 연령 집단을 변수로 설정한 것이지만, 이것을 시간적으로 확장할 수 있다. 즉, 특정 연도의 연령 집단을 변수로 설정하는 대신, 전연령 플로와 같은 단일 속성에 대해 연도를 확장하는 것이다(Elmes and Harris, 1996). 그러나 속성의 준거가 연령 집단 혹은 연도처럼 반드시 하나일 필요는 없다. 연령 집단과 연도를 결합한 복합 준거로 다이아딕 매트릭스의 속성을 구성할 수도 있다. 즉, 특정 연도의 연령 집단과 함께 다른 연도의 연령 집단도 함께 병렬적으로 배열하는 방식이다(Yan and Thill, 2009). 또 다른 확장 방식으로는, 아예 변수를 특정 연도 간의 변화량으로 치환하는 것이다. 즉, 하위 인구 집단별로 특정 두 연도 사이의 변화량을 계산하고, 그 변화량을 변수로 설정하는 것이다. 이렇게 다양한 방식으로 다이아딕 매트릭스를 확장할 수 있다면, 그것은 자동적으로 다이아딕 PCA 기법의 확장을 의미하는 것이 된다. 또 다른 의미의 확장성은 다른 분석 기법과의 연계 가능성이다. 이런 측면에서 이성분트렌드매핑(bicomponent trend mapping, BTM)(Schroeder, 2010; 김현미･이상일, 2021) 기법과의 결합 가능성을 하나의 예로 제시할 수 있을 것이다. BTM은 기본적으로 지역별 시공간적 역동성 분석 도구로 개발된 것인데, 인구이동의 연구에서도 충분한 적용성을 가진다는 연구 결과를 보면(Li et al., 2014), 인구이동 플로의 시공간적 역동성을 탐색하는 데도 충분히 적용될 수 있을 것으로 보인다.

본 연구는 공간적 상호작용 데이터에 대한 지리학적 연구가 보다 활성화되기를 바라는 의도로 기획된 것이다. 이는 에드워드 울만이 공간적 상호작용 개념을 ‘지리학에 통일성을 부여하는 프레임(unifying frame for geography)’으로 간주한(Hepple, 2009, 713), 바로 그 관점의 가치를 현 시점에서 되살리는 것일 수 있다. 더 나아가 인문지리학의 다양한 하위 분야에서 분리되어 연구되어 온 것들이 ‘공간적 상호작용론(spatial interaction studies)’이라고 하는 보다 큰 우산 아래에서 보다 통합적으로 다루어지기를 기대하는 의도도 깔려 있다(유사한 시도로 허우긍 등, 2015를 들 수 있다). 예를 들어, 본 연구의 초점인 인구이동은 인구지리학의 전통적인 연구 주제이지만, 본 연구에서 제시된 분석 프레임워크를 도시지리학의 전통적인 주제인 통근 연구에 적용하지 못할 이유는 전혀 없는 것이다. 공간적 상호작용 데이터의 다양성과 이용가능성이 전에 없이 고양된 현 시점을 전제할 때, 보다 정교한 방법론으로 무장한 공간적 상호작용 현상에 대한 지리학적 연구는 지리학의 본연적 가치를 고양하는데 특별한 역할을 할 수 있다고 믿는다. 본 연구가 “공간적 상호작용론이라고 하는 인문지리학의 통섭적 하위 분야에서 방법론적 차용과 주제적 융합을 진작하는”(이상일, 2012) 하나의 시도로 평가되기를 기대한다.

주

1) 사실 통계청의 보도자료에 나타나 있는 시군구 수준의 이동률에 대한 통계값에는 오류가 있다(표 1에 부가되어 있는 참고 표). 시군구 수준의 인구이동은 ‘시도간 이동’에 ‘시도내 이동’ 중 ‘시군구간 이동’을 합산해서 구한다. 그런데 통계청의 보도자료의 해당 표를 보면, 2015년까지는 올바른 값을 제공하고 있으나, 2016년 이후의 연도에 대해서는 시군구 수준의 이동률에 대해 ‘시도내 이동’ 전체의 이동률을 제시하는 오류를 범하고 있다. 해당 표에서 시군구 컬럼과 시도 컬럼의 합계는 절대로 총이동 컬럼의 값과 같을 수 없다. 2016~2020년의 시군구 수준 이동률(%)의 올바른 값은 각각 8.9, 8.7, 8.8, 8.7, 9.4이다.

2) 시군구 단위에서 살펴보면, 경기 수원시 → 경기 화성시(21,536명), 경기 고양시 → 경기 파주시(14,1132명), 경기 성남시 → 경기 용인시(13,497명), 경기 수원시 → 경기 용인시(11,848명), 경기 성남시 → 경기 광주시(11,556명) 등 모두 경기도 내의 시 지역간 이동이 주를 이룬다.